Fórmulas matriciales: Curso de Matrices en Excel para aprender a trabajar con rangos en vez de con celdas con la finalidad de trabajar con datos organizados en rangos más rápidamente.

Temario: trabajar con rangos matriciales: operaciones básicas y función SI(). Fórmulas de resumen de rangos matriciales: SUMA(), CONTAR(), PROMEDIO(). Uso de SUMA(SI()) para contar. CONTAR.SI() matricial. Funciones matriciales específicas: FRECUENCIA(), TENDENCIA() y SUMAPRODUCTO(). Funciones SI CONJUNTO. Lógica Matricial.

 

Descarga los ejemplos en: https://www.dropbox.com/s/p3ots7xugziesd6/Excel-Matrices.zip?dl=0

Puedes ir al índice de contenidos para ver todos los Minicursos.

Usando fórmulas y funciones matriciales podemos hacer las mismas cosas que una tabla dinámica y las funciones BD juntas, pero con más potencia.

 

Desconocer el funcionamiento de las matrices en Excel no es algo malo. La gran mayoría de la gente usa Excel sin saber nada de matrices y lo usan muy bien. Pero si alguna vez el jefe te pide que hagas una cuenta de cuántas personas han hecho menos de tres cursos en un año, sin repetir la persona, o cuales son los clientes con compras más cercanas a 10.000, tal vez resuelvas el problema en una hora haciendo filtros, extracciones y conteos, o tal vez lo resuelvas en cinco minutos usando alguna fórmula matricial sacada de internet.

Las fórmulas matriciales se diferencian de las fórmulas normales en que operan con rangos, llamados aquí matrices. Es decir, estamos acostumbrados a, por ejemplo, a multiplicar A3*B5, o a usar la función SI() con celdas, como por ejemplo SI(A2>3;…..). Pero con las funciones matriciales podremos multiplicar rangos como A5:B10*C5:D10, o podemos aplicar una función SI() a un rango entero como =SI(A1:B100>3;…..). Otra diferencia es que se suelen introducir con CONTROL + MAYUSCULAS + ENTER (CTRL + SHIFT + ENTER) en vez de con un ENTER normal.

 

Las funciones matriciales nacieron de la necesidad de trabajar con listas y hacer resúmenes sobre ellas que de otra manera serían más complicados, sino imposibles.

 

Qué diferencia hay pues entre un "rango" y una "matriz"

La palabra "matriz" se diferencia de la palabra "rango" en lo siguiente:

"Matriz" se considera un conjunto ordenado de elementos. En términos de Excel, una matriz es un rango de una columna o de una fila (matriz unidimensional) o un rango rectangular (matriz bidimensional). Por tanto, a primera vista un rango y una matriz son lo mismo.

El quid de la cuestión, es que Excel tiene muy en cuenta el orden en que están colocados los datos dentro del rango. Para dos rangos diferentes, X e Y, Excel, al considerarlos una matriz, relaciona la primera celda del rango X con la primera celda del rango Y, la segunda celda del rango X con la segunda celda del rango Y, la tercera celda del rango X con la tercera celda del rango Y, etcétera.

 

Por tanto, usualmente el tamaño de los rangos de una operación matricial han de ser iguales y se han de colocar los datos en los rangos ordenados por algún criterio, por tanto, son ideales para utilizar con las listas ordenadas de datos.

 

Los 4 tipos de fórmulas matriciales

Microsoft subdivide las fórmulas matriciales en dos tipos: las fórmulas matriciales multicelda y las fórmulas matriciales unicelda. Nosotros, en este Minicurso solamente, haremos cuatro subdivisiones de las fórmulas matriciales, que llamaremos simplemente: matrices de Tipo 1, matrices de Tipo 2, matrices de Tipo 3 y matrices de Tipo 4, tal cual sin más complicaciones. No es preciso que entiendas ahora mismo lo que significan estos 4 tipos, porque no es fácil:

• TIPO 1: Una misma fórmula en las celdas de un rango. Ocupan varias celdas y se introducen con CONTROL + MAYUSCULAS + ENTER. Para crear este tipo de fórmulas matriciales debes primero seleccionar un rango, teclear una fórmula y acabar con CONTROL + MAYUSCULAS + ENTER, entonces Excel rellena todo el rango con la misma fórmula automáticamente. Equivalen a una fórmula multicelda según la subdivisión de Microsoft. Se usan poco pero son necesarias para entender las fórmulas matriciales de Tipo 2.
• TIPO 2: Fórmulas de resumen. Ocupan una sola celda y se introducen con CONTROL + MAYUSCULAS + ENTER. Para crear este tipo de fórmulas matriciales debes hacer clic en una celda, teclear una fórmula y acabar con CONTROL + MAYUSCULAS + ENTER. La fórmula ha de contener una función de resumen, es decir, un conteo, una suma, un promedio... Equivalen a una fórmula unicelda según la subdivisión de Microsoft. Son las que más se usan y es necesario conocer las de Tipo 1 para entenderlas.
• TIPO 3: Funciones estándar con comportamiento matricial. Ocupan una sola celda y se introducen con ENTER, como cualquier fórmula estándar. Para crear este tipo de fórmulas matriciales debes hacer clic en una celda, teclear una fórmula y acabar con ENTER. La fórmula es una función estándar pero que se comporta de modo matricial de por sí. Básicamente es la función SUMAPRODUCTO().
• TIPO 4: Fórmulas matriciales de Tipo 2 ó 3 que se crean en una celda y luego se copian en un rango de celdas con el cuadro de relleno. Es lo mismo que hacemos con las funciones normales. Lo importante es que no deben confundirse con fórmulas de Tipo 1. En estos casos hay que tener en cuenta cómo se ponen los $ en los rangos.
  

 

Solamente cuando acabes de entender las fórmulas matriciales del Tipo 2 (Fórmulas de resumen), será cuando empieces a hacerte una idea clara de la utilidad de las fórmulas matriciales. Antes no, por tanto, habrás de tener un poco de paciencia.

 

 

Características básicas de las fórmulas matriciales

• En las fórmulas matriciales, si se cambian los valores de los rangos afectados, cambia el resultado automáticamente. Esto es igual que las funciones normales.
• Las funciones matriciales suelen ser poco usadas, por lo que debe evitarse su uso cuando una hoja de cálculo vaya dirigida a otras personas. En cambio, son una herramienta excelente cuando se trata de analizar características complejas que afectan a rangos de datos, por ejemplo, contar cuantos elementos sin repetir hay en una lista de datos.
• En vez de usar rangos normales (por ejemplo A1:F7), puedes usar nombres de rangos, creados con la funcionalidad CTRL-F3.
• Como hemos dicho, las fórmulas matriciales se suelen introducir con CONTROL + MAYUSCULAS + ENTER (CTRL + SHIFT + ENTER) en vez de con un ENTER normal.

 

Operadores y funciones matriciales

Quizás estés temiendo ver unas funciones rarísimas con nombres inextricables. Pues no. Veamos:

• Los operadores matriciales son los mismos operadores normales de toda la vida: +, -, *, /. Estamos acostumbrados a operar con A3*C2, pero usados matricialmente permiten hacer cosas como A10:B10*D10:F10, o, si tenemos rangos nombrados, nombrerango1*nombrerango2.
• También están los operadores lógicos matriciales para usar en la función SI() que también son los de siempre: =, >, <, >=, <=, <>, sin embargo, las funciones Y(), O(), NO() no se pueden usar en fórmulas matriciales.
• En cuanto a las funciones matriciales son casi todas las funciones normales, por ejemplo, hemos visto que la función SI() puede comportarse de manera normal o de manera matricial. Para que Excel sepa que una función normal la queremos usar como función matricial, debemos acabar la fórmula con CONTROL + MAYUSCULAS + ENTER (CTRL + SHIFT + ENTER) en vez de con un ENTER normal.
• Cuando es necesario poner varias pruebas lógicas en un SI() matricial, hay que usar SI() anidados o bien productos y sumas de funciones lógicas como se explicará más adelante. No obstante, a partir de Excel 2007, se añadieron unas funciones denominadas SI CONJUNTO que facilitan mucho la tarea de usar varias pruebas lógicas en una función SI().
• Otras funciones como FRECUENCIA()sí que son funciones especiales que solamente se pueden usar matricialmente, no se puede usar como funciones normales. Son del tipo 1: necesitan un rango para aplicarse y acabar con CONTROL+MAYUSCULAS+ENTER. La función TENDENCIA() es recomendable usarla como Tipo 1, si bien se puede usar como función de Tipo 3.
• Otras funciones específicamente matriciales que requieren previamente seleccionar un rango son MDETERM(), MINVERSA(), MMULT() y otras, pero no las veremos aquí ya que son funciones matriciales aritméticas, o sea, se usan para hacer operaciones con matrices, pero el tipo de matrices que estudiábamos en la escuela.

 

 

En inglés queda más claro, ya que este tipo de fórmulas se denominan "array formulas", entendiendo "array" (en inglés, "en hileras" o "en filas") como "un conjunto de datos dispuestos en filas" o "un conjunto de datos en arreglo tabular", es decir, lo que en Excel se denomina "una lista". Este es el tipo de matrices del que hablaremos en este Minicurso.

 

En cambio, en inglés se denomina "matrix" (en plural "matrixes/matrices") a las matrices aritméticas que estudiábamos en la escuela y de las que no hablaremos nada en este Minicurso.

 

 

Funciones matriciales de resumen

Tampoco son funciones especiales o raras. Son las de siempre. Como función de resumen para una operación matricial lógica se puede usar SUMA(), CONTAR(), PROMEDIO(). Es importante saber que CONTARA() como función de resumen matricial no se puede usar, así que solamente podremos contar números con CONTAR(), pero se explicará un truco para evitar este inconveniente. Las funciones matriciales de resumen se introducen en una sola celda y se pone como parámetros de dichas funciones otra operación matricial aritmética o lógica. Entonces esa fórmula resumirá todo el rango afectado. Se terminan también con CONTROL+MAYUSCULAS+ENTER.

Las funciones matriciales de resumen en Excel son pues, casi todas las funciones normales que puedan usarse para resumir datos, nosotros usaremos las siguientes:

SUMA(), PROMEDIO(), CONTAR(), MAX(), MIN(), recordar que CONTARA() no se puede usar de manera matricial.

Tocaremos en especial SUMA(SI()), CONTAR(SI()), PROMEDIO(SI()) ya que se usan mucho, también veremos SUMA(SI(ESERROR())) etc…

 

Funciones que tienen un comportamiento matricial de por sí

Se introducen con un ENTER normal, pero operan con rangos como si fuesen funciones matriciales. Por ejemplo:

SUMAPRODUCTO(), SUMAR.SI(), CONTAR.SI()

Y hay más, pero que nosotros no usaremos, ya que son para operaciones matriciales aritméticas de las que estudiábamos en la escuela, como SUMAX2MASY2(), SUMAX2MENOSY2(), SUMAXMENOSY2(), COVAR() y otras.

 

Uso de las funciones y operadores matriciales

Tienen dos usos, el primero es trabajar con matrices matemáticas, como las que hacíamos cuando íbamos a la escuela, pero esto no lo tocaremos aquí ya que es un uso muy especializado. El otro uso es obtener resultados resumen de muchos rangos en una sola celda.

Suele ocurrir que quien se acostumbra a usar las matrices las encuentra cómodas de usar.

 

Las fórmulas matriciales, son elementos indispensables para convertirse en usuario avanzado de Excel. Son una de las herramientas más poderosas de Excel y adquirir dominio de ellas permitirá realizar cálculos complejos con facilidad.

 

¿Cómo se distinguen las funciones matriciales de las normales?

No se distinguen en nada las funciones y operadores normales de las funciones y operadores matriciales, lo que hace la distinción es que las funciones y operadores normales se introducen tecleando y acabando con ENTER, las funciones y operadores matriciales introducen tecleando y acabando con CONTROL+MAYUSCULAS+ENTER, que se refiere a pulsar a la vez las siguientes teclas del teclado:

 

 

Nota: en un teclado Mac también es válido usar  + MAYÚS + ENTRAR.

 

Como resultado las fórmulas se ven entre llaves { } pero esas llaves no las ponemos nosotros, las pone Excel al pulsar CONTROL+MAYUSCULAS+ENTER. Por ejemplo:

 

 

 

Constantes matriciales

Se usan rara vez, pero lo explicamos aquí por si acaso. En las fórmulas normales, podemos normalmente multiplicar A3*7 siendo 7 una constante. Pues bien, al igual que en las fórmulas normales podemos incluir estos valores constantes, en las fórmulas matriciales también podemos incluir valores constantes que se los denomina constantes matriciales. Estas constantes matriciales son matrices, y deberemos ponerlas entre llaves { y } (esta vez sí que tecleamos nosotros estas llaves) e incluir un separador de columnas (símbolo ;) y un separador de filas (símbolo \).

Por ejemplo, supongamos que tenemos estos datos en una hoja de cálculo:

 

 

Y yo quiero multiplicar lo siguiente: Primera fila: el 3 (B2) lo quiero multiplicar por 10; el 5 (C2) lo quiero multiplicar por 20; Segunda fila: el 7 (B3) lo quiero multiplicar por 30; el 9 (C3) lo quiero multiplicar por 40. Pues entonces lo que hay que hacer es:

=B2:C3*{10;20\30;40}

O sea, la constante matricial es: abrir llave, 10, separador de columna (;), 20, separador de fila (\), 30, separador de columna (;) 40 y cierra llave.

Y esto da como resultado:

 

 

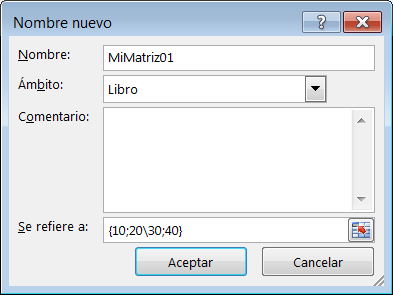
A las constantes matriciales se les puede dar un nombre con la funcionalidad CTRL-F3. Por ejemplo:

 

 

Entonces podríamos usar la fórmula matricial:

=B2:C3*MiMatriz01

 

Todo esto explicado parece difícil, pero se aclarará cuando veamos unos ejemplos.

 

Basta de teoría y comencemos con los temas prácticos.

 

_{Continua en la siguiente entrega. Puedes también ir al Indice de los Minicursos o Volver arriba.}