Fórmulas y Funciones Matriciales en Excel.
Funciones más útiles para crear fórmulas matriciales en Excel. Parte 2.
Fórmulas matriciales: Curso de Matrices en Excel para aprender a trabajar con rangos en vez de con celdas con la finalidad de trabajar con datos organizados en rangos más rápidamente.
Temario: trabajar con rangos matriciales: operaciones básicas y función SI(). Fórmulas de resumen de rangos matriciales: SUMA(), CONTAR(), PROMEDIO(). Uso de SUMA(SI()) para contar. CONTAR.SI() matricial. Funciones matriciales específicas: FRECUENCIA(), TENDENCIA() y SUMAPRODUCTO(). Funciones SI CONJUNTO. Lógica Matricial.
Descarga los ejemplos en: https://www.dropbox.com/s/p3ots7xugziesd6/Excel-Matrices.zip?dl=0
Puedes ir al índice de contenidos para ver todos los Minicursos o a la primera entrega de este minicurso de Matrices en Excel.
Funciones más útiles en el mundillo de las fórmulas matriciales de Excel
Fórmulas matriciales que dan resultados correctos incluso si los rangos tienen errores: CONTAR(SI(ESERROR())), SUMA(SI(ESERROR())), PROMEDIO(SI(ESERROR()))…
Las funciones de información en Excel son un grupo de funciones que devuelven VERDADERO o FALSO según una celda cumpla un criterio o no. Otras funciones de información devuelven otros valores.
Estas funciones son:
| Función | Descripción |
CELDA() |
(no disponible en OneDrive) Retorna información acerca del formato, la ubicación o el contenido de una celda. |
ES.IMPAR() |
Retorna VERDADERO si el número es impar. |
ES.PAR() |
Retorna VERDADERO si el número es par. |
ESBLANCO() |
Retorna VERDADERO si el valor está en blanco. |
ESERR() |
Retorna VERDADERO si el valor es cualquier valor de error excepto #N/A. |
ESERROR() |
Retorna VERDADERO si el valor es cualquier valor de error. |
ESFORMULA() |
(desde Excel 2013) Retorna VERDADERO si existe una referencia a una celda que contiene una fórmula. |
ESLOGICO() |
Retorna VERDADERO si el valor es un valor lógico. |
ESNOD() |
Retorna VERDADERO si el valor es el valor de error #N/A. |
ESNOTEXTO() |
Retorna VERDADERO si el valor no es texto. |
ESNUMERO() |
Retorna VERDADERO si el valor es un número. |
ESREF() |
Retorna VERDADERO si el valor es una referencia. |
ESTEXTO() |
Retorna VERDADERO si el valor es texto. |
HOJA() |
(desde Excel 2013) Retorna el número de la hoja a la que se hace referencia. |
HOJAS() |
(desde Excel 2013) Retorna la cantidad de hojas en una referencia. |
INFO() |
(no disponible en OneDrive) Retorna información acerca del entorno operativo en uso. |
N() |
Retorna un valor convertido en un número. |
NOD() |
Retorna un error #N/A. Se usa para forzar que una fórmula retorne #N/A cuando nos interesa que dé error. |
TIPO() |
Retorna un número que indica el tipo de dato de un valor. |
TIPO.DE.ERROR() |
Retorna un número que corresponde a un tipo de error. |
De todas ellas, nos fijaremos en la función lógica de información ESERROR(celda), que devuelve VERDADERO si una celda contiene un error (#N/A #¡VALOR! #¡REF! #¡DIV/0! #¡NUM! #¿NOMBRE? #NULO). Es una función estándar pero también es matricial, por tanto, puede ir bien dentro de una función matricial de Tipo 1 y, por consiguiente, de Tipo 2. Como Tipo 2, es útil para ser usada con rangos de datos que contienen errores, de manera que podemos hacer que la función de resumen ignore los errores y dé un resultado basado solamente en los valores no erróneos.
Vamos a verlo.
Seguimos en el archivo "MasUsadasEnMatrices.xls" en la hoja "Errores".
La columna D tiene la fórmula columna B ÷ columna C. Observa que en el rango D6:D13 hay errores de división por cero, y la fórmula estándar =PROMEDIO(D6:D13) que hay en D14 no nos es útil.
Para solucionar esto, usaremos una función matricial de Tipo 2 en D15. Haz lo siguiente:
- Haz clic en D15
- Teclea la fórmula
=PROMEDIO(SI(ESERROR(D6:D13);"";D6:D13)) - Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado debería ser:
113.810,10
Dentro de la función de resumen PROMEDIO() matricial de Tipo 2, hemos puesto la función matricial de Tipo 1 SI(ESERROR(D6:D13);"";D6:D13). Esta función SI() recorre el rango D6:D13 retornando a PROMEDIO() solamente los valores sin error que encuentra en ese rango ya que, si encuentra un error, retorna un valor nulo "". Es importante poner un nulo "" en el segundo parámetro de la función SI(), ya que un valor "" no influye en el cálculo de un promedio, de una suma, de un conteo, etc. Es decir, podemos usar:
- Para un promedio
=PROMEDIO(SI(ESERROR(D6:D13);"";D6:D13)) - Para una suma
=SUMA(SI(ESERROR(D6:D13);"";D6:D13)) - Para un conteo
=CONTAR(SI(ESERROR(D6:D13);"";D6:D13)) - etc.
Todas las funciones de información pueden usarse en funciones matriciales, por ejemplo para contar en la celda C18 cuantos textos hay en la columna B puedes hacer esto:
- Haz clic en C18
- Teclea la fórmula
=SUMA(SI(ESTEXTO(B1:B1000);1)) - Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado debería ser:
5
Observa que hemos usado el truco que vimos en un tema anterior de usar la función SUMA() para contar.
Funciones SUMA(K.ESIMO.MAYOR()), SUMA(K.ESIMO.MENOR()) a partir de la versión Excel 97
Las funciones K.ESIMO son fáciles de entender, si se explica bien lo que hacen. Tienen esta sintaxis:
=K.ESIMO.MAYOR(matriz;lugar)
y
=K.ESIMO.MENOR(matriz;lugar)
Ambas funciones operan con un rango de valores como primer parámetro.
K.ESIMO.MAYOR() retorna, de ese rango de valores, el valor que estaría en un cierto lugar si ese rango estuviese ordenado de mayor a menor, es decir, por ejemplo, ¿qué valor estaría en el 8º lugar si ese rango lo ordenásemos de mayor a menor? Si el rango estuviese en A1:A100 entonces la función =K.ESIMO.MAYOR(A1:A100;8) retornará el valor ocuparía el 8º lugar si hubiésemos ordenado A1:A100 de mayor a menor.
K.ESIMO.MENOR() hace exactamente lo mismo, pero suponiendo que ese rango estuviese ordenado de menor a mayor. Así, la función =K.ESIMO.MENOR(A1:A100;21) retorna el valor que ocuparía el 21º lugar si hubiésemos ordenado A1:A100 de menor a mayor.
K.ESIMO.MAYOR() y K.ESIMO.MENOR() nos permiten ahorrarnos de tener que ordenar un rango para trabajar con él, con lo que podemos trabajar con rangos desordenados como si estuviesen ordenados.
Nota: el segundo parámetro de estas funciones indica un lugar, no indica un valor: no sirven para obtener un segundo o tercer valor más grande o un segundo o tercer valor más pequeño dentro de un rango. Sirven para obtener qué valor habría en el segundo o tercer lugar dentro de un rango si lo ordenásemos de mayor a menor, o de menor a mayor. Es lo que en inglés se llama un Ranking por posiciones. Por ejemplo, supón que un rango ordenado de mayor a menor queda así: 3, 2, 2, 2, 2, 2, 1, entonces el lugar nº 6 de este rango es 2 (3, 2, 2, 2, 2, 2, 1). Si el rango lo ordenásemos de menor a mayor quedaría así: 1, 2, 2, 2, 2, 2, 3, entonces el lugar nº 4 de este rango es también 2 (1, 2, 2, 2, 2, 2, 3).
Las funciones K.ESIMO.MAYOR() y K.ESIMO.MENOR() son funciones matriciales de Tipo 3 de por sí. Se puede saber porque, en la ayuda contextual que aparece cuando tecleas una fórmula en Excel, aparece la palabra "matriz":
... y se introducen con un ENTER normal. Sin embargo, dado que el segundo parámetro no es una matriz, sino que es solamente un número que indica un lugar, en la práctica no sirve de mucho que sean funciones matriciales. Por consiguiente, se usan mucho en fórmulas de resumen Tipo 2 introduciéndolas con CONTROL+MAYUSCULAS+ENTER.
Como siempre, antes de ver su uso como Tipo 2, vamos a ver su uso como Tipo 1.
Como funciones de Tipo 1 nos permite extraer datos ordenados de un rango no ordenado y, como Tipo 2, resumir tales datos. Por ejemplo ¿cómo obtengo la suma de los números que ocupan los cinco primeros lugares en un rango si este rango estuviese ordenado de mayor a menor? Para resolverlo, veremos primero la función K.ESIMO.MAYOR() como Tipo 1.
Vamos a verlo. Seguimos en el archivo "MasUsadasEnMatrices.xls" en la hoja "Kesimos":
Funciones K.ESIMO como funciones matriciales multicelda de Tipo 1
Supón que te piden que obtengas los números del rango B3:C17 que ocuparían los cinco primeros lugares si lo ordenásemos de mayor a menor. Observa que B3:C17 está desordenado y además no se puede ordenar por medios normales ya que ocupa dos columnas. En las celdas E3:E7 están puestos ya los números de 1 a 5 que son los lugares (ranking) que te están pidiendo. Sigue estos pasos:
- Selecciona el rango desde F3 hasta F7
- Sin clicar en ningún sitio para que no se deshaga la selección, teclea la fórmula:
=K.ESIMO.MAYOR(B3:C17;E3:E7)
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado:
Si quieres comprobar que es correcto, no te quedará más remedio que comprobar a ojo que es así, mirando todos los números que hay en B3:C17, ya que como hemos dicho, no podemos ordenar datos dispuestos en dos columnas de manera convencional.
Funciones K.ESIMO como funciones matriciales unicelda de Tipo 2
Sería el caso de si te piden que sumes esos cinco primeros números. Podemos hacerlo sin usar rangos intermedios con datos visibles usando una fórmula matricial Tipo 2. Sigue estos pasos:
- Haz clic en J10
- Teclea la fórmula
=SUMA(K.ESIMO.MAYOR(B3:C17;E3:E7))
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado es:
231
Puedes comprobar que es correcto sumando el rango F3:F7, si bien el rango F3:F7 ya no es necesario. Lo puedes borrar pues recuerda que las fórmulas matriciales de Tipo 2 no necesitan rangos intermedios con datos visibles.
Pero atención, no es del todo cierto que no hayamos usado rangos intermedios con datos visibles, porque hemos usado el rango E3:E7 que contiene los números 1 a 5, que son los lugares que nos han pedido. ¿Qué podemos hacer para evitar tener que poner este rango externo?
La solución es usar una constante matricial. Como se vio en la Introducción a este Minicurso, una constante matricial se construye así:
- encerrar la matriz entre llaves { y } tecleadas manualmente
- separar los números por punto y coma.
En este caso la constante matricial sería: {1;2;3;4;5} y la fórmula habría que modificarla así:
- Selecciona el rango desde E3 hasta E7
- Pulsa la tecla SUPR para borrar su contenido. Como resultado la fórmula en J10 muestra un error
- Haz clic en J10
- Teclea o modifica la fórmula así:
=SUMA(K.ESIMO.MAYOR(B3:C17;{1;2;3;4;5}))
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
El error desaparece y J10 vuelve a mostrar el resultado correcto:
231
Comprueba asimismo que, cambiando los números del rango B3:C17, el resultado en J10 también cambia. Por ejemplo, cambia B3 por un 999 y observa que la suma también cambia a 1189. Te recordamos que el rango B3:B17 sigue sin estar ordenado.
Sin embargo, hay un problema. Si en un momento dado te piden que sumes los números que están en los 100 primeros lugares de un rango sin ordenar, estarías obligado a teclear la constante matricial {1;2;3;4;5;6;7; ... ;98;99;100}, es decir, una constante matricial de ¡100 números!
Afortunadamente, Excel proporciona la función =FILA(1:100) que te evitará tener que teclear esa constante matricial de 100 números, si bien esto es válido solamente para constantes matriciales de una sola fila (recuerda que las constantes matriciales pueden tener varias filas separadas por una contrabarra "\").
La función FILA() usada no matricialmente tiene otros usos, pero ahora nos interesa ver solamente su uso matricial, ya que nos va a permitir sustituir la constante matricial {1;2;3;4;5} por la función FILA(1:5), o bien la constante matricial {1;2;3;4;5;6;7; ... ;98;99;100} por la función FILA(1:100), etc. Sigue estos pasos:
- Haz clic en B3
- Vuelve a introducir su valor inicial de 6 (J10 vuelve a ser 231)
- Haz clic en J12
- Teclea la siguiente fórmula:
=SUMA(K.ESIMO.MAYOR(B3:C17;FILA(1:5)))
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
J12 muestra igualmente el resultado correcto:
231
Si quieres saber la suma de los números que ocuparían los 15 primeros lugares del rango B3:C17 si estuviese ordenado de mayor a menor, haz lo siguiente:
- Haz clic en J14
- Teclea la siguiente fórmula:
=SUMA(K.ESIMO.MAYOR(B3:C17;FILA(1:15)))
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado en J14 es:
543
Nota: si alguna vez has de usar la función FILA() dentro de una función matricial de Tipo 4, es decir, varias fórmulas matriciales de resumen de Tipo 2 pero tecleando solamente la primera y copiando el resto con el cuadro de relleno, recuerda que hay que poner $ a la primera fórmula para usar referencias absolutas. La función FILA(1:5) en formato de referencia absoluta sería FILA($1:$5).
Funciones K.ESIMO como funciones matriciales de Tipo 3
Por último, y dado que estrictamente hablando estas dos funciones son de Tipo 3 que se introducen con un simple ENTER siempre y cuando el segundo parámetro no sea un rango, vamos a ver cómo usarlas como Tipo 3, que en realidad es igual que usarlas como Tipo 1 pero de manera más sencilla. Esta vez veremos las dos funciones K.ESIMO.MAYOR() y K.ESIMO.MENOR(). Supón que te piden que obtengas los números del rango B3:C17 que ocuparían los cinco primeros lugares si lo ordenásemos de mayor a menor y, asimismo, los valores que ocuparían los cinco primeros lugares si lo ordenásemos de menor a mayor.
- Vuelve a rellenar el rango E3:E7 con los valores 1, 2, 3, 4 y 5:
- Haz clic en F3
- Teclea la fórmula
=K.ESIMO.MAYOR($B$3:$C$16;E3) - Acaba con un ENTER normal
- Vuelve a hacer clic en F3
- Copia la fórmula hasta F7 con el cuadro de relleno, bien arrastrándolo bien haciéndole doble clic
- Haz clic en G3
- Teclea la fórmula
=K.ESIMO.MENOR($B$3:$C$16;E3) - Acaba con un ENTER normal
- Vuelve a hacer clic en G3
- Copia la fórmula hasta G7 con el cuadro de relleno, bien arrastrándolo bien haciéndole doble clic
El resultado final debería ser:
Comprueba asimismo que, cambiando los números del rango B3:C17, el resultado en F3:G7 también cambia. Por ejemplo, cambia B3 por un 99 y C3 por un -99 y observa que los valores en F3:G7 también cambian. Te recordamos que el rango B3:B17 sigue sin estar ordenado.
Funciones matriciales que se usan como Tipo 1
Vamos a ver las funciones FRECUENCIA() y TENDENCIA(). La función FRECUENCIA() solamente se puede usar como función matricial de Tipo 1 y no puede ser usada de otra manera. Siempre ha de introducirse con CONTROL+MAYUSCULAS+ENTER. La función TENDENCIA() es mejor usarla como Tipo 1, si bien también puede usarse como Tipo 3 acabada con ENTER normal.
Función FRECUENCIA() para obtener la distribución de frecuencias de unos valores de un rango
La función FRECUENCIA() solamente puede usarse como una fórmula matricial de Tipo 1, lo que nos obligará a seleccionar un rango antes de teclearla e introducirla con CONTROL+MAYUSCULAS+ENTER. No se puede usar de otra manera. Esta función hace un conteo de cuántos números hay dentro de rango, pero es un conteo desglosado en intervalos. Su sintaxis es:
=FRECUENCIA(rango a contar;rango con los intervalos en que desglosamos el conteo)
Enseguida verás que, para que puedas usar esta función, deberás seleccionar un rango del mismo tamaño que el segundo parámetro, entonces tendrás que teclear la fórmula y acabar con CONTROL+MAYUSCULAS+ENTER.
Seguimos en el archivo "MasUsadasEnMatrices.xls" en la hoja "Resúmenes". Nos centraremos ahora en la zona de la hoja a partir de la celda J10:
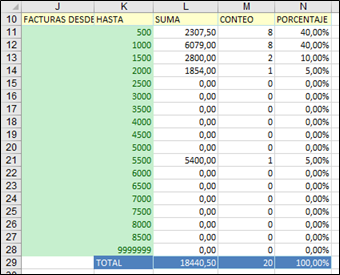
Supón que te piden que cuentes cuántos números hay dentro del rango E2:E21. A simple vista ya vemos que hay 20 números, pero te piden que desgloses, de esos 20 números, cuántos números hay entre 0 y 100, cuántos hay entre 100 y 200, cuántos hay entre 200 y 300, cuántos hay entre 300 y 400... en concreto, te piden que desgloses dicho conteo según los intervalos que hay en el rango desde J11 hasta K28. Haz lo siguiente:
- Selecciona desde M11 hasta M28
- Teclea la fórmula
=FRECUENCIA(E2:E21;K11:K28) - Acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado:
El conteo desglosado empieza en M11 y significa lo siguiente: hay 1 factura cuya cantidad está entre 0 y 100 euros, 2 facturas cuya cantidad está entre 100 y 200 euros, 1 factura cuya cantidad está entre 200 y 300 euros, 2 facturas cuya cantidad está entre 300 y 400 euros, etc… En la celda M29 está la suma de estos conteos desglosados. Esta suma es 20 que es justamente el conteo que habíamos hecho a simple vista mirando el rango E2:E21.
Este "conteo desglosado en intervalos" se denomina en estadística "distribución de frecuencias por categorías".
Si quieres, puedes ir cambiando los números del rango E2:E21 y verás como cambia automáticamente este conteo desglosado (o distribución de frecuencias), pero la suma en M29 siempre ha de dar 20.
Observa que te hemos dicho que queremos un conteo de facturas distribuido según los intervalos (o categorías) que hay en el rango J11:K28, pero en la función FRECUENCIA() no hemos usado para nada la columna J. Solamente hemos usado la columna K, la que tiene los límites superiores de las categorías y, aun así, la fórmula ha dado resultados correctos. Esto es debido a que la función FRECUENCIA() solamente necesita los límites superiores de las categorías en que queremos distribuir el conteo. Para comprobarlo haz lo siguiente:
- Selecciona el rango desde J11 hasta J28
- Pulsa la tecla SUPR para borrar su contenido
La columna M sigue dando los mismos valores lo que demuestra que la columna J no es necesaria. Solamente habíamos puesto la columna J para que los intervalos quedasen más claros a los ojos de un usuario. Así pues, la distribución que hay a partir de la celda M11 que ha hecho la función FRECUENCIA() es la siguiente:
- Hay 1 factura cuya cantidad es menor o igual a 100 euros
- Hay 2 facturas cuya cantidad está entre 100 euros exclusive y 200 inclusive
- Hay 1 factura cuya cantidad está entre 200 euros exclusive y 300 inclusive
- Hay 2 facturas cuya cantidad está entre 300 euros exclusive y 400 inclusive
- etc…
Por tanto, a la hora de hacer el cálculo, la función FECUENCIA() toma en cuenta cada celda del rango K11:K28 pero también la celda inmediatamente superior, y es por eso que esta función ha de ser siempre de Tipo 1.
Los números que queremos que la función FRECUENCIA() desglose, se ponen en el primer parámetro de la función, en este caso es el rango E2:E21.
Para que quede más claro, fíjate que la cantidad que hay en E2 es de 200 euros ¿en cuál de las categorías o intervalos está incluida la cantidad de 200? Mira como está ahora la distribución:
Haz clic en E2 y teclea 200,01. El resultado:
Hemos resaltado en amarillo las celdas que han cambiado. La categoría "Hasta 200" ha disminuido en 1 unidad mientras que la categoría "Hasta 300" ha aumentado en 1 unidad, esto significa que la cantidad de 200 euros estaba incluida en la categoría "Hasta 200" porque "Hasta 200" significa en realidad "Desde 100 exclusive hasta 200 inclusive" y, cuando hemos cambiado a 200,01 esta cantidad ha pasado a la categoría "Desde 200 exclusive hasta 300 inclusive".
Ahora haz clic en E2 y teclea 199,99. El resultado vuelve a ser igual que cuando E2 contenía el valor 200:
... porque 199,99 es una cantidad incluida en la categoría "Desde 100 exclusive hasta 200 inclusive".
Ahora haz clic en E2 y teclea el número negativo -9999. Resaltamos en amarillo los valores que cambian:
Esto significa que la primera categoría "Hasta 100" significa en realidad "Desde cualquier valor negativo hasta 100 inclusive".
Resumiendo: M11 muestra el conteo desde cualquier valor negativo hasta 100 inclusive, M12 desde 100 exclusive hasta 200 inclusive, M13 desde 200 exclusive hasta 300 inclusive, M14 desde 300 exclusive hasta 400 inclusive, etc.
Observa que con este sistema de no usar la columna J, no nos podemos equivocar en las categorías y la función FRECUENCIA() siempre hará bien la distribución de los números, de modo que, por mucho que cambies los números que hay desde E2 hasta E21, la celda M29 siempre mostrará 20, aunque los valores mostrados desde M11 hasta M28 vayan cambiando.
Observa también que, como hemos dicho, como función matricial de Tipo 1, antes de teclear la fórmula hay que seleccionar un rango tan grande como el rango con los intervalos o categorías (en este caso K11:K28), en cambio, el otro rango, el rango E2:E21, de donde la función FRECUENCIA() toma las cantidades en euros a distribuir en esos intervalos o categorías, puede ser del tamaño que se quiera.
Si te piden la distribución en porcentajes, usa la fórmula que ponemos a continuación:
- Haz clic en E2
- Introduce el valor 200
- Selecciona el rango N11:N28
- Teclea la fórmula
=FRECUENCIA(E2:E21;K11:K28)/CONTAR(E2:E21)
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado:
Sin embargo, si en vez de un conteo, te piden que distribuyas la suma de los números que están dentro de esos intervalos o categoría, la función FRECUENCIA() ya no nos es útil. Hay que usar la función de resumen SUMAR.SI.CONJUNTO() como fórmula matricial de Tipo 4: crear la primera fórmula con los $ adecuadamente colocados y copiándola con el cuadro de relleno. Sigue estos pasos:
- Haz clic en E2
- Introduce el valor 200
- Haz clic en L11
- Teclea la fórmula:
=SUMAR.SI(E2:E21;"<="&K11)
- Y acaba con un ENTER normal. Es una función de Tipo 3 pero no es todavía la primera de las funciones de Tipo 4 con los $ adecuadamente colocados porque la primera fórmula es distinta de las demás. Ni siguiera hemos usado
SUMAR.SI.CONJUNTO() - Haz clic en L12
- Teclea la fórmula:
=SUMAR.SI.CONJUNTO($E$2:$E$21;$E$2:$E$21;">"&K11;$E$2:$E$21;"<="&K12)
- Y acaba con un ENTER normal. Es una función de Tipo 3 y esta sí que ya es la primera de las funciones de Tipo 4 con los $ adecuadamente colocados y, dado que requiere más de 1 criterio, ya hemos usado
SUMAR.SI.CONJUNTO() - Vuelve a hacer clic en L12 y copia la fórmula arrastrándola por el cuadro de relleno hasta L28.
El resultado debería ser:
Tal como dijimos que hay que hacer en las fórmulas de Tipo 4, la primera fórmula que tecleemos ha de tener los $ adecuadamente colocados. Observa que en L29 está el total de totales de las facturas distribuidas en los intervalos o categorías. Esta suma necesariamente ha de coincidir con la suma de los valores del rango E2:E21. Asimismo, la celda M29 contiene la suma del conteo por categorías, que necesariamente ha de coincidir con el conteo de los valores del rango E2:E21. Por último, la celda N29 necesariamente ha de sumar 100% si los porcentajes están bien calculados.
Como curiosidad, en Excel 2003, para calcular las sumas distribuidas por las categorías, hay que usar SI() anidados, debido a que no existen en Excel 2003 las funciones SI CONJUNTO. La primera de las fórmulas de resumen de Tipo 4 (celda L12) tendría que haber sido en Excel 2003:
=SUMA(SI($E$2:$E$21>J11;SI($E$2:$E$21<=K11;$E$2:$E$21))) y CONTROL+MAYUSCULAS+ENTER
Por último, si te piden que uses intervalos de 500 en vez de intervalos de 100, rellena el rango desde K11 hasta K27 con los valores 500, 1000, 1500... (no cambies el 9999999 que hay en K28) El resultado:
Si trabajas con valores muy grandes, deberás cambiar el valor 9.999.999 que hay en K28.
Es importante tener en cuenta siempre que esta función solamente puede usarse como Tipo 1. Si no se hace así, mostrará valores erróneos pero sin mostrar ningún mensaje de error específico.
Función TENDENCIA() para predecir valores futuros a partir de valores presentes (tema opcional)
La función TENDENCIA() suele usarse como una fórmula matricial de Tipo 1, pero, de hecho, a diferencia de FRECUENCIA(), también puede usarse como Tipo 3. Esta función nos permite saber la tendencia de una serie de valores sin necesidad de hacer un gráfico a partir de esos valores y trazar su línea de tendencia. Su sintaxis es:
=TENDENCIA(rango de valores conocidos;rango de períodos conocidos;rango de períodos futuros a predecir)
Los rangos del 1er y 2o parámetros han de ser iguales. Debe seleccionarse un rango del mismo tamaño que el 3er parámetro, teclear la fórmula y acabar con CONTROL+MAYUSCULAS+ENTER. Sin embargo, si el 3er parámetro no es un rango sino solamente una celda, puede acabarse la fórmula con ENTER normal.
Es una fórmula de poco uso, más bien financiero o estadístico. Básicamente sirve para predecir, en base a los valores actuales, si en el futuro, de seguir la tendencia actual, esos valores crecerán o decrecerán. Puede servir para hacer previsiones, por ejemplo.
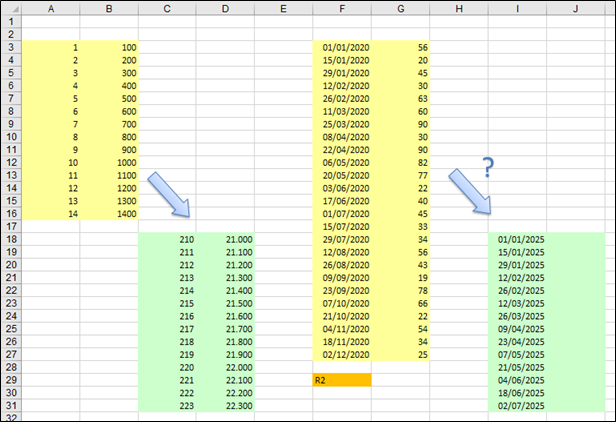
Vamos a verlo con un ejemplo muy obvio. Seguimos en el archivo "MasUsadasEnMatrices.xls" en la hoja "Tendencia":
Haz clic en D18 y observa que ya hemos puesto la fórmula matricial de Tipo 1:
{=TENDENCIA(B3:B16;A3:A16;C18:C31)}
- El 1er rango B3:B16 contiene los valores ya conocidos, usualmente cantidades de dinero de ingresos, cantidades de dinero de gastos, una medición de lluvias, crecimiento de bacterias o algo similar. Estos datos se denominan "históricos" o "registros".
- El 2o rango A3:A16 contiene los períodos de esos valores ya conocidos. Los "períodos" son una numeración secuencial 1, 2, 3, 4, 5... que indica días, meses, años o lo que se quiera. Usualmente indican el paso del tiempo, aunque también puede ser una numeración secuencial pero no de tiempo, por ejemplo, gramos de azúcar en un cultivo de bacterias.
- El 3er rango C18:C31 contiene los períodos futuros que queremos predecir. Nuevamente, los "períodos" son una numeración secuencial, pero con el mismo significado que el 2o rango, es decir, días, meses, años... pero ha de ser un rango de períodos situado en el futuro. En este caso hemos usado los períodos 210, 211, 212, 213... y, como hemos dicho, también podrían ser los gramos de azúcar para los que queremos predecir el crecimiento o decrecimiento de un cultivo de bacterias.
- El rango D18:D31 es el rango que hemos seleccionado antes de teclear la fórmula
TENDENCIA()de Tipo 1 y es el rango donde queremos que Excel calcule los valores futuros que queremos predecir. La funciónTENDENCIA()nos permitirá saber si los valores actuales tienen tendencia a crecer o a decrecer. - Por último, hemos introducido la fórmula con CONTROL+MAYUSCULAS+ENTER.
En este ejemplo concreto, los valores registrados (B3:B16) van desde 100 hasta 1400, y los períodos de tiempo (A3:A16) son desde el 1 hasta el 14. Pongamos que esto significa que, en los 14 primeros meses de vida de nuestra empresa, hemos tenido unos ingresos de 100 el mes 1, de 200, el mes 2, de 300 el mes 3... Está bien claro los ingresos mensuales de nuestra empresa son crecientes. Si asumimos que esa tendencia se va a mantener con el paso del tiempo ¿cuáles serán los ingresos futuros en los meses 210 hasta 223 de la vida de nuestra empresa? Si miráis los valores del rango desde D18 hasta D31 veréis lo que era muy claro, que la tendencia es creciente:
Con este ejemplo, muy obvio, hemos visto que la fórmula muestra resultados futuros si sigue esa tendencia.
La función
TENDENCIA()es una función estadística inferencial (= que hace estimaciones futuras), que se usa mucho como función financiera. Pero también puede usarse como función estadística descriptiva (= que describe los datos históricos o registrados) simplemente para tener claro si esos valores registrados son decrecientes, estables o crecientes. Una tendencia tiene tres clasificaciones: a corto plazo, a medio plazo o a largo plazo. Tiene tres direcciones: al alza, sostenida o a la baja. Por ejemplo, una tendencia calculada a largo plazo puede ser al alza, pero esa misma tendencia calculada a corto plazo puede ser a la baja. En finanzas, suele ser mejor no usar todos los valores históricos registrados para calcular la tendencia, sino solamente los valores máximos o los valores mínimos (denominados "puntos de inflexión") de entre todos esos valores históricos. Sin embargo, en finanzas se prefiere dibujar la tendencia en forma gráfica.
Por consiguiente, la función TENDENCIA() puede usarse como descriptiva y, en tal caso, no es necesario calcular todos los períodos, basta con calcular un solo período. En este caso, se usaría como Tipo 3. Seguimos en el archivo "MasUsadasEnMatrices.xls" en la hoja "Tendencia". Haz lo siguiente:
- Selecciona el rango D18:D31
- Pulsa la tecla SUPR para borrar su contenido
- Haz clic en la celda D18
- Teclea la fórmula (hemos destacado en color la parte que hemos cambiado):
=TENDENCIA(B3:B16;A3:A16;C18)
- y acaba con un ENTER normal.
El resultado:
El valor que aparece en la celda D18 es exactamente el que había antes en esta misma celda, pero, si te fijas, con este valor ya tenemos suficiente para saber que los datos históricos tienen tendencia al alza. No necesitamos más. Hemos usado la función TENDENCIA() como función descriptiva en vez de predictiva. En este caso, podríamos haber sustituido la función TENDENCIA() por una función más eficiente en velocidad de cálculo que es PRONOSTICO() para Excel 2013 y anteriores o PRONOSTICO.LINEAL() para Excel 2016 y posteriores. No las explicaremos aquí.
Nota: La función TENDENCIA() siempre hace una inferencia lineal y=a∙x+b basada en el método de los mínimos cuadrados. Excel tiene otras funciones que se usan de idéntica manera que TENDENCIA() pero que usan otros métodos de cálculo. Por ejemplo, la función CRECIMIENTO() hace una inferencia exponencial y=b∙ax basada en el método de la linealización por logaritmos.
Vamos a ver un ejemplo menos obvio que el anterior. Vamos a usar la función TENDENCIA() para que Excel infiera si, en base a los períodos y valores históricos que hay en el rango F3:G27, hay tendencia al alza o a la baja en los períodos futuros que hemos puesto en el rango desde I18 hasta I31. Fíjate que en este caso hemos usado fechas para los períodos en vez de números. Esto puede hacerse porque, en Excel, las fechas no son más que números con un formato de fecha. Haz lo siguiente:
- Primero observa los datos históricos del rango F3:G27 y atrévete a hacer una inferencia por ti mismo: de seguir con esta tendencia ¿la tendencia futura es al alza o a la baja?
- Una vez que hayas hecho la inferencia por ti mismo, comprueba si has acertado. Vamos a usar
TENDENCIA()como fórmula matricial de Tipo 1. Selecciona el rango desde J18 hasta J31. - Sin hacer clic en ningún sitio para que no se deshaga la selección, teclea la fórmula:
=TENDENCIA(G3:G27;F3:F27;I18:I31)
- Y acaba con CONTROL+MAYUSCULAS+ENTER.
El resultado:
Vemos entonces que, no solamente hay tendencia decreciente, sino que en el futuro los resultados serán negativos.
No obstante, siempre es recomendable verificar si este resultado es fiable o no. Esto se hace con la función estándar COEFICIENTE.R2(). Esta función calcula el denominado "coeficiente de determinación" o "R cuadrado" que es un valor que, expresado en porcentaje, está entre 0% y 100%. Se considera que si este valor es menor que 75%, los datos históricos tienen poca relación entre sí. Por ejemplo, vamos a ver si este último cálculo que hemos hecho es fiable. Haz lo siguiente:
- Haz clic en G29
- Teclea la fórmula
=COEFICIENTE.R2(G3:G27;F3:F27)(observa que el cálculo se hace sobre los datos históricos o registrados) - Acaba con ENTER (es una función estándar)
El resultado debería ser:
El resultado está muy por debajo del 75%, lo que significa que los datos históricos no tienen relación alguna entre sí y por tanto la tendencia calculada es no fiable. Es fácil comprobarlo, haz clic en G27 e introduce el valor 56 (el mismo que hay en G3 al inicio del rango de datos históricos). La tendencia cambia totalmente.
Aquí hemos puesto un ejemplo concreto de períodos y valores, como si fuesen datos económicos, pero la función TENDENCIA() puede usarse para cualquier tipo de pronóstico de dos elementos que cumplan algún tipo de relación. Puede usarse también para calcular períodos en el pasado o para interpolar. Por ejemplo, si los períodos conocidos van de 10 en 10, puedo interpolar calculando con TENDENCIA() esos mismos períodos pero de 1 en 1.
Continua en la siguiente entrega. Puedes también ir al Indice de los Minicursos o Volver arriba.























0 comentarios:
Publicar un comentario